1. The Basics of Unsupervised Clustering
Unsupervised clustering is a powerful technique used in various fields to identify patterns and group similar data points together without any prior knowledge or labels. It is particularly useful when we have a large dataset and want to discover hidden structures or relationships within the data.
There are several unsupervised clustering algorithms available, each with its own strengths and weaknesses. One commonly used algorithm is K-means clustering, which aims to partition the data into a predetermined number of clusters based on the similarity of data points. Another popular algorithm is hierarchical clustering, which builds a tree-like structure of clusters by iteratively merging or splitting clusters based on their similarity.
In practice, the choice of clustering algorithm depends on the nature of the data and the specific problem at hand. K-means clustering is often preferred when the number of clusters is known or can be estimated, while hierarchical clustering is more flexible and can handle situations where the number of clusters is unknown.
Unsupervised clustering finds applications in various domains, such as customer segmentation, anomaly detection, image segmentation, and document clustering. By identifying similar groups within a dataset, unsupervised clustering helps in gaining insights, making data-driven decisions, and improving the understanding of complex systems.
In the next section, we will discuss the importance of measuring clustering performance and introduce the widely used Within-Cluster Sum of Squares (WCSS) metric and the Elbow method. While the Elbow method is a classic approach for determining the optimal number of clusters, it can sometimes be challenging to pinpoint the exact elbow point. We will explore a refinement to the Elbow method that addresses this limitation and helps in picking the right number of clusters more accurately.
2. Evaluating Clustering Performance: The Elbow Method
Measuring clustering performance is crucial to determine the effectiveness and quality of the clustering results. One commonly used metric is the Within-Cluster Sum of Squares (WCSS), which measures the compactness or tightness of the clusters. WCSS calculates the sum of squared distances between each data point and its centroid within a cluster. The goal is to minimize the WCSS, as smaller values indicate that the data points within each cluster are more similar to each other.
To determine the optimal number of clusters, the Elbow method is often employed. The Elbow method plots the WCSS against the number of clusters and looks for the point where the rate of improvement in WCSS significantly decreases. This point is referred to as the “elbow” and suggests that adding more clusters does not lead to substantial improvement in clustering performance (Plot 1).
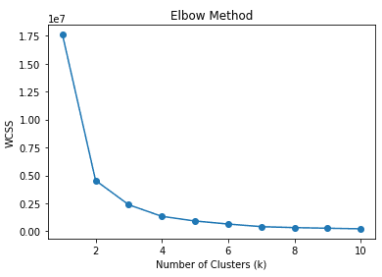
However, identifying the exact elbow point can be challenging, as the plot may not exhibit a clear elbow shape. In some cases, the curve may be smooth and gradual, making it difficult to determine the optimal number of clusters. In a recent project, I have been trying to cluster short expressions. Extracting trigram letters as features, we obtain a couple thousand sparse features. The number of clusters could range from 40 to several hundreds. In this project, it is very difficult to see an elbow in the WCSS plot (Plot 2).
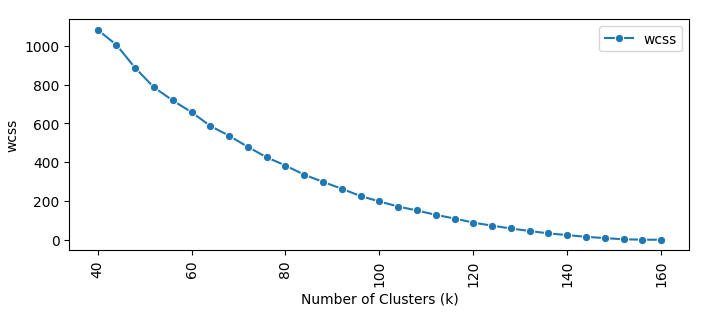
In the following section, we will explore a refinement to the Elbow method that addresses this limitation. This refinement introduces a new metric: the decrease in WCSS per number of added clusters. By examining the marginal improvement in WCSS for each additional cluster, we can gain a clearer understanding of the transition between significant improvement and slower improvement. This refinement helps in picking the right number of clusters more accurately, even in cases where the elbow point is not obvious.
3. Enhancing the Elbow Method: A New Metric for Cluster Performance
To further enhance the accuracy of determining the optimal number of clusters, a refinement on the Elbow method introduces a new metric: the decrease in Within-Cluster Sum of Squares (WCSS) per number of added clusters. You can think of this as the marginal improvement (i.e. decrease) in WCSS for each added cluster. This metric provides valuable insights into the marginal improvement in WCSS for each additional cluster (Table 1).
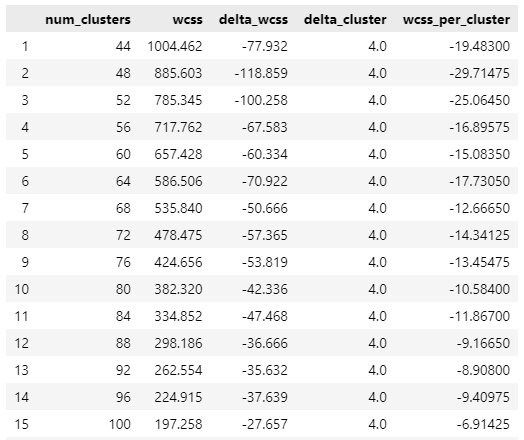
Plotting the new metric, we can see a clear transition between significant improvement and slower improvement. This refinement allows us to pinpoint the number of clusters that result in substantial enhancement in clustering performance (Plot 3).
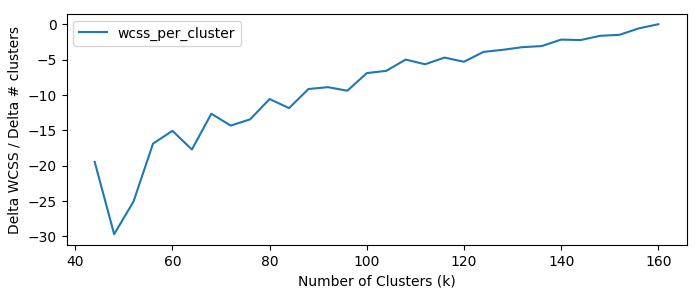
The new metric helps address the limitation of the Elbow method, particularly when the plot does not exhibit a clear elbow shape. In such cases, the curve may appear smooth and gradual, making it challenging to determine the optimal number of clusters. However, with the introduction of the decrease in WCSS per number of added clusters, we can identify the point where the improvement in clustering performance starts to diminish significantly. In this example (Plot 4), we see that beyond 60 clusters there is a diminishing return and adding more clusters does not reduce WCSS as much as initially.
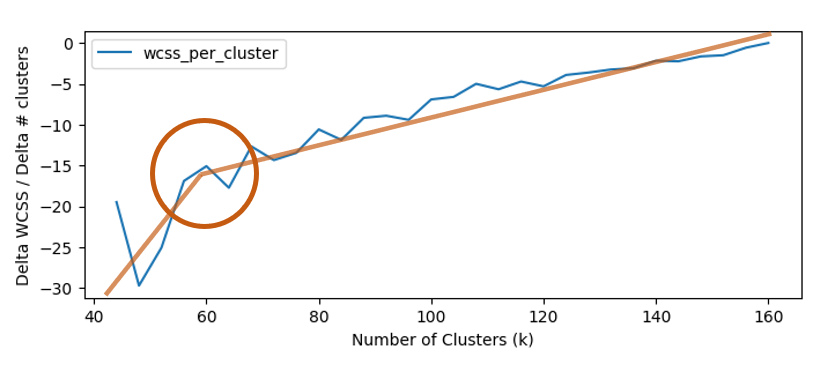
By utilizing this refined approach, we can confidently choose the right number of clusters, even in situations where the elbow point is not obvious. This improvement enhances the accuracy and reliability of unsupervised clustering algorithms, enabling data analysts and researchers to make more informed decisions based on the clustering results.
4. Final Thoughts on Enhancing the Elbow Method
In summary, we present an improvement on the Within-Cluster Sum of Squares (WCSS) metric to better identify the optimal number of clusters for your unsupervised clustering algorithm. By refining the Elbow method and introducing a new metric, the decrease in WCSS per number of added clusters, we can overcome the limitations of the traditional Elbow approach and make more accurate decisions regarding the number of clusters to use.
The new metric allows us to examine the improvement in clustering performance as clusters are added, helping us identify the point where the improvement starts to diminish significantly. This refinement provides valuable insights into the marginal improvement in WCSS for each additional cluster, enabling us to pinpoint the precise number of clusters that result in substantial enhancement in clustering performance.
With this improved approach, even in cases where the elbow point is not obvious or the curve appears smooth and gradual, we can confidently choose the right number of clusters. This enhancement enhances the accuracy and reliability of unsupervised clustering algorithms, empowering data analysts and researchers to make more informed decisions based on the clustering results.
By incorporating this refined method into your clustering analysis, you can ensure that you are utilizing the optimal number of clusters for your specific dataset, leading to more meaningful and accurate insights.
Happy Data Science!
Further Reading:
- Elbow Method for Finding the Optimal Number of Clusters in K-Means
Written by Basil Saji — Published On January 20, 2021
In-depth description of the elbow approach to selecting the number of clusters - Stop Using Elbow Method in K-Means Clustering
Written by Anmol Tomar, Published on Aug. 02, 2023
Another alternative to elbow, the silhouette coefficient

Leave a Reply